细粉加工设备(20-400目)
我公司自主研发的MTW欧版磨、LM立式磨等细粉加工设备,拥有多项国家专利,能够将石灰石、方解石、碳酸钙、重晶石、石膏、膨润土等物料研磨至20-400目,是您在电厂脱硫、煤粉制备、重钙加工等工业制粉领域的得力助手。
超细粉加工设备(400-3250目)
LUM超细立磨、MW环辊微粉磨吸收现代工业磨粉技术,专注于400-3250目范围内超细粉磨加工,细度可调可控,突破超细粉加工产能瓶颈,是超细粉加工领域粉磨装备的良好选择。
粗粉加工设备(0-3MM)
兼具磨粉机和破碎机性能优势,产量高、破碎比大、成品率高,在粗粉加工方面成绩斐然。
如图,已知三角形ABC内角于圆O,角BAC=120度,AB=AC,BD
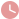
.jpg)
如图, ABC内接于⊙O,∠BAC=120°,AB=AC,BD为 ⊙O
答案 如图, ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则BC= 6 A C B D 0 [考点]圆周角定理;解直角三角形 [分析]由已知可证∠BDA=30°;根据BD为⊙O的直径,可 如图,三角形ABC内接于⊙O,角BAC=120度,AB=AC,BD为⊙O的直 如图,三角形ABC内接于⊙O
.jpg)
如图所示,在 ABC中,∠BAC=120°,AD平分∠BAC交BC于D,求
2009年8月27日 — 如图:过C作CE//AD,并于BA的延长线交于E,则易证 ACE为等边三角形,于是:AB/AD=AE/EC=(AB+AE)/EC 因为AE=AC,EC=AC代入得: AB/AD 如图所示,圆O是三角形ABC的外接圆,角BAC与角ABC的平分线相交于点I,延长AI交圆O与点D,连接BD,DC 若圆O的半径为10cm,角BAC=120度求三角形BAC面积的最大值如图所示,圆O是三角形ABC的外接圆,角BAC与角ABC的平分

如图,在三角形ABC中,角BAC=120度,AB=AC,点D在BC上
1、角dae=105度 因为角BAC=120度,AB=AC,所以角abc和acb相等等于30度, 所以叫acb=180度20度=150度,所以角cae=角cea=15度, 又因为bd=da,所以角dba=角dab=30 2014年2月23日 — 简单的数学问题如图,三角形abc内接于圆o,ab等于bc,角abc等于120度,ad为圆o的直径解:∵AB=BC,∠ABC=120° ∴∠C=(180°120°)÷2=30° ∴∠D=30° ∵AD 简单的数学问题如图,三角形abc内接于圆o,ab等于bc,角abc等于120

如图,已知三角形abc是圆o的内接三角形,ab=ac,点p是弧ab
2014年5月2日 — 如图,已知三角形abc是圆o的内接三角形,ab=ac,点p是弧ab的中点,连接pa,pb,pc解:(1)∵∠BPC=60°, ∴∠BAC=60°, ∵AB=AC, ∴ ABC为等边三角形, 2017年12月16日 — 如图,三角形ABC是圆o的内接等腰三角形,顶角角BAC等于36度,弦BD、CE分别平分角ABC、角证明:∵AB=AC,∴∠ABC=∠ACB, 如图,三角形ABC是圆o的内接等腰三角形,顶角角BAC等于36度,弦BD
.jpg)
如图已知,三角形ABC内接于圆o,弦BC所对的劣弧为120度角ABC,角
2013年3月2日 — 如图已知,三角形ABC内接于圆o,弦BC所对的劣弧为120度角ABC,角ACB的平分线BD,CE分别交AC于D交AB于E,1)解:∵劣弧BC的度数 2014年9月17日 — (2014?常德)如图,已知 ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=80∵ ABC三个内角的平分线交于点O,∴∠ACO=∠BCO,在 COD和 COB中,CD=CB∠OCD=∠OCBCO=CO,∴ COD≌(2014?常德)如图,已知 ABC三个内角的平分线交于点O
.jpg)
已知:如图,在 ABC中,AB=AC,点D,E分别在边AC
已知:如图,在 ABC中,AB=AC,点D,E分别在边AC,AB上,且∠ ABD=∠ ACE,BD与CE相交于点O求证:(1)OB=OC;(2)BE=CD (1)证明:∵AB=AC, ∴∠ABC=∠ACB; ∵∠ABD=∠ACE, ∴∠OBC=∠OCB, ∴OB=OC (2)证明:如图, A E D 2011年11月2日 — 如图,在三角形ABC中,AB=AC,角BAC=120度,AC的垂直平分线EF交AC于点E,交BC于点F,求证:BF=2CF证明:连接AF∵EF是AC的垂直平分线∴AF=CF∵∠BAC=120°,AB=AC∴∠B=∠C=30°∴∠C=∠CAF=30°∴∠BAF=90 如图,在三角形ABC中,AB=AC,角BAC=120度,AC的

如图,在三角形ABC中,角BAC=120度,AB=AC,点D在BC上
如图,在三角形ABC中,角BAC=120度,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA 1试求角DAE的度数 2如果把试题中AB=AC的条件去掉,其余条件不变,那么角DAE的度数会改变吗?为什么?1 如图所示,圆O是三角形ABC的外接圆,角BAC与角ABC的平分线相交于点I,延长AI交圆O与点D,连接BD,DC若圆O的半径为10cm,角BAC=120度求三角形BAC面积的最大值 2 如图所示,圆O是三角形ABC如图所示,圆O是三角形ABC的外接圆,角BAC与角ABC的平分
.jpg)
如图,在三角形ABC中,AB=AC,作业帮
因为 AB=AC,角A=36度 所以 角ABC=角ACB=72度 因为 CD平分角ACB 所以 角BCD=角DCA=36度 因为 角A=36度 所以 角BCD=角A 因为 角DBC=角ABC 所以 三角形CDB相似于三角形ABC 所以 AB/BC=BC/BD 因为 角DCA=36度,角A=36度 所以 角DCA=角A2021年10月28日 — 如图,已知在三角形ABC中,角BAC等于90度,AB=AC,点D在边BC上,以AD为边作正方形ADEF,联结CF,CE(1)求证FC垂直于BC(2)如果BD=AC,求证 如图,已知在三角形ABC中,角BAC等于90度,AB=AC,点D在边BC上,以AD为边作正方形ADEF,联结CF,CE(1)求证FC垂直于BC(2)如果BD=AC,求证CD=CE 展开如图,已知在三角形ABC中,角BAC等于90度,AB=AC,点D在

如图所示,在三角形ABC中,角ABC=90度,AC=BC,D为
(1)证明:如图,连接CD,交AB于点F,AD=BD点C和点D均在线段AB的垂直平分线上直线CD为线段AB的垂直平分线为等腰直角三角形(2)如(1)中图所示若,则线段AE的长为1(1)连接CD,交AB于点F,则由线段垂直平分线的判定定理可得,直线CD是线段AB的 如图,在等腰三角形ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;② OPC是等边三角形;③AC=AO+AP;④ABC OCP S =S四边形其中所有正确结论的序号为( )P AB D A ①②③如图,在等腰三角形ABC中,AB=AC,∠BAC=120°,AD⊥
.jpg)
《圆》的计算及证明题之中考真题精选汇编(1) 百度文库
3.如图,圆内接四边形ABCD的对角线AC,BD交于点E,BD平分∠ABC,∠BAC=∠ADB 4.如图,已知⊙O是等边三角形ABC的外接圆,连接CO并延长交AB于点D,交⊙O于点E,连接EA,EB . (1)写出图中一个度数为30°的角:,图中与 ACD全等的 2010年1月17日 — 已知 如图三角形ABC中,AB=AC,角BAC=90度当且仅当BD为角ABC的角平分线时CD=1/ 2BE延长CD与BA的延长线交于F 显然EDFA四点共圆=>角AEB=角CFA AB=AC 已知 如图三角形ABC中,AB=AC,角BAC=90度百度知道
.jpg)
如图,在三角形ABC中,AB=AC,点D在边AB上,且AD
1 A DB C如图,在三角形ABC中,AB=AC,点D在边AB上,且AD=DC=BC.求三角形ABC各内角的度数. 2 如图,在三角形ABC中,AB=AC,点D在边AB上,且AD=DC=BC.求三角形ABC各内角的度数.2014年9月6日 — 已知:如图, ABC内接于⊙O,BC=12cm,∠A=60°.求⊙O的直径解:如右图所示,连接OB、OC,并过O作OD⊥BC于D,∵OD⊥BC,BC=12,∴BD=CD=6,∵∠A=60°,∴∠BOC=120°,∵OB=OC,OD⊥BC,∴∠BOD=∠COD=60 已知:如图, ABC内接于⊙O,BC=12cm,∠A=60°.求⊙O
.jpg)
【题文】已知:如图,在 ABC 中, AB = AC, AB 的垂直
【解析】 【分析】 (1)根据线段垂直平分线的性质可得EA=EB,进一步即可求得结果; (2)先根据等腰三角形的性质和三角形的内角和定理求出∠ABC的度数,再利用等边对等角求出∠EBA的度数,即可求出结果 【详解】 解:(1)∵DE是AB的垂直平分线,∴EA=EB, 2016年12月2日 — 三角形ABC的外角角ACD的平分线CP与内角角ABC的平分线BP交于点P,已知角BPC=40度。(1)若角ABC=角ACB,则角BAC=?(要步骤)(2)求角CAP的度数 三角形ABC的外角角ACD的平分线CP与内角角ABC的平分线BP交于点P,已知角三角形ABC的外角角ACD的平分线CP与内角角ABC的平分

如图,在 ABC中,∠ ACB=90°,AC=BC,点D是线段BC边
如图,在 ABC中,∠ ACB=90°,AC=BC,点D是线段BC边上的一点,连结AD,点E在射线BC上,过E作EF⊥ AD交AD于点F (1)如图1,当D是BC的中点,且DF=BD时,若AB=4√2,求CE的长;(2)如图2,当CE=CD时,延长EF交AB于点G,取AD的中点H,连结EH,过点A作AM ∥ BE,交EH的延长线于点M,猜想AM与BG之间的数量关系并证明2018年4月24日 — 已知: ABC外接于圆O,∠BAC=60°,AE⊥BC,CF垂直AB。AE、CF相交于点H,点D为弧BC的中点。连接HD,AD。求证: AHD为等腰三角形。 已知: ABC外接于圆O,∠BAC=60°,AE⊥BC,CF垂直AB。已知: ABC外接于圆O,∠BAC=60°,AE⊥BC,CF垂直AB

如图三角形ABC内接于圆O,∠BAC=120°,AB=AC,BD为圆O的
2014年1月7日 — 如图三角形ABC内接于圆O,∠BAC=120°,AB=AC,BD为圆O的直径,AD=6,求DC长因为三角形ABC中,角BAC=120度,且AB=AC,所以角ABC=角BCA=30度,所以角BDA=30度,又因为BD是圆的直径,所以角BAD=90度,再因为角BDA=角BCA=30 百度首页 2013年1月7日 — 已知:如图 ABC内接于⊙O,∠BAC的平分线AD交⊙O于点D,交边DC于点E,联结BD证明:因为AD是角BAC的角平分线所以:角BAD=角DAC因为:角DBC与角DAC都是狐DC所对的角所以,角DAC=角DBC 所以,角BAD=角DBC 所以,三角形BDE已知:如图 ABC内接于⊙O,∠BAC的平分线AD交⊙O于点D,交

如图,已知 ABC,以BC为直径的⊙O交AB于点D,点E为的中点
2.如图,已知 ABC,以BC为直径的⊙O交AB于点D,点E为BD的中点,连结CE交AB于点F,且AF=AC.(1)判断直线AC与⊙O的位置关系,并说明理由;(2)若⊙O的半径为2,sinA=45,求CE的长.A DE FB C2011年10月4日 — 如图,三角形ABC内接于圆O,连接OA,OC。若AB=AC,弧BC为100度,求角AOC和弧AC的度数连接AO因为AB=AC;BO=OC;AO=AO所以,三角型AOB全等于三角型AOC所以,角AOB=角AOC所以角AOC=(360100 )/2=130度所以弧AC的度 如图,三角形ABC内接于圆O,连接OA,OC。若AB=AC
.jpg)
已知 ABC是⊙O的内接三角形,AB=AC=2,∠BAC=120°求⊙
2011年2月11日 — 已知 ABC是⊙O的内接三角形,AB=AC=2,∠BAC=120°求⊙O直径的长您要看着好请采纳,多谢。方法一:连接OA,OB,OC。因为OA=OB=OC,且AB=AC,所以两个等腰三角形AOB和AOC全等。所以角OBA=角OAB=角OAC=角ACO。又因为角2013年2月22日 — 如图,三角形ABC内接于圆O,AD平分角BAC交圆O于D,DE垂直AB于E1)延长AB到F,使得BF=AC,连DF,CD因为AD平分BAC所以∠BAD=∠CAD所以BD=CD因为∠FBD=∠ACD,BF=AC所以 BDF≌ CDA所以DF=DA因为DE⊥AF所以EF=AE,因为EF=EB+如图,三角形ABC内接于圆O,AD平分角BAC交圆O于D
.jpg)
如图,三角形ABC中,角BAC=120度,AD垂直BC于D,且AB+BD
2018年3月21日 — 如图,三角形ABC中,角BAC=120度,AD垂直BC于D,且AB+BD=DC,求角C的度数 (用两种方法)方法1:延长DB至E使得BE=BA,则DE=DB+BE=DB+BA=DC,易证ADE全等于ADC,AC=AE,所以三角形ACE为等腰三角形 ,角AEB=角C又,角ABC=角A 【答案】分析:由AB+BD=DC,易想到可作辅助线DE=DB,然后连接AE,从而可出现两个等腰三角形,一个是 ABE,一个是 ACE,利用三角形外角的性质,易求∠B=2∠C,再利用三角形内角和定理可求∠C. 解答: 解:在DC上截取DE=DB,连接AE,设∠C=x,∵AB+BD=DC,DE=DB,∴CE=AB,又∵AD⊥BC,DB=DE,如图,在 ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD

如图,在 ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD
2018年3月7日 — 如图,在 ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,那么∠C=度解:在DC上截取DE=DB,连接AE,设∠C=x,∵AB+BD=DC,DE=DB,∴CE=AB,又∵AD⊥BC,DB=DE,∴直线AD是BE的垂直平分线,∴AB=AE,∴CE=AE 如图,已知AB是半径为1的圆O的一条弦,且AB=a<1,以AB为一边在圆O内作正三角形ABC,点D为圆O上不同于点A的一点,且DB=AB=a,DC的延长线交圆O于点E , 百度试题 如图,已知AB是半径为1的圆O的一条弦,且AB=a<1,以

如图,在 ABC中,∠BAC=120°,P为 ABC内一点,求证
2016年11月13日 — 如图,在 ABC中,∠BAC=120°,P为 ABC内一点,求证:PA+PB+PC>AB+AC证明:以AC为边向外作正 ACE,则E在BA延长线上,且BE=AB+AC,再以AP为边作正 APQ,使B、Q位于AP两旁,连结QE在 APC与 如图,已知三角形ABC中,角BAC=90度,AB=AC,AE是过A的一条直线,且B、C在A、E的异侧,BD垂直AE于D,CE垂直AE于E,试说明:BD=DE+CE 百度试题 结果1如图,已知三角形ABC中,角BAC=90度,AB=AC,AE是过A的一
.jpg)
如图,已知三角形ABC内接于圆O,角C=45度,过点O作OD垂直
2012年12月9日 — 如图圆o是三角形abc的外接圆,ab为直径,od平行bc交圆 24 如图,在 ABC中,AB=AC,以AB为直径作⊙O,交BC于 25 如图,已知三角形ABC内接于⊙O,角C=45°,弦AB的弦心 15 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点D,OA2013年12月19日 — 如题AB=AC,∠BAC=20,∠BDC=30得到∠ACD=10°与等边对等角相矛盾。 若AB=AC,∠A=20°,AD=BC。求得∠BDC=30°。解:过A点作CD的垂线交CD的延长线于点E,作AF⊥BC,垂足为F。 在 AEC和 CFA中 ∵∠E=∠AFC=90°∠ECA=∠FAC,AC=AC如图,三角形ABC中,AB=AC,∠BAC=20,∠BDC=30,求证

如图:在 ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于
2016年5月4日 — 如图:在 ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF证明:(1)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,∴DE=DC,又∵BD=DF,∴Rt CDF≌Rt EBD(HL).∴CF=EB;(2)∵AD 是∠BAC的平分线,D 2018年4月12日 — 在三角形ABC中,AB=AC,角A=100度,BD平分角ABC求证:AD+BD=BC解:∵∠A=100° 且AB=AC∴∠ABC=∠ACB=40°又∵DB平分∠ABC ∴∠ABD=∠DBC=20°且∠ADB=60° 延长BD到E点,使DE=AD,在BC上找一点F,使BF=AB得 在三角形ABC中,AB=AC,角A=100度,BD平分角ABC求证
.jpg)
【题目】 如图,⊙ O 是 ABC 的外接圆,∠ BAC = 45 °, AD
【题目】 如图,⊙ O 是 ABC 的外接圆,∠ BAC = 45 °, AD ⊥ BC 于点 D ,延长 AD 百度试题 如图,⊙O是 ABC的外接圆,∠BAC=45°,AD⊥BC于点D,延长AD交⊙O于点E,若BD=4,CD=1,则DE的长是 A0D BC E 答案 415 2 相关推荐 2013年6月6日 — 题目应该是这样的吧: 如图,在 ABC中,∠BAC=120°,以BC为边向外作等边 BCD,把 ABD绕点D按顺时针方向旋转60°后到 ECD的位置。若AB=3,AC=2,求∠BCD的度数和AD的长。在三角形ABC中,角BAC=120度,以BC为边向形外作等边三角
.jpg)
已种只对具报理百清热打后统如图,已知等腰三角形ABC
已种只对具报理百清热打后统如图,已知等腰三角形ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上 10.(3分)已知如图等腰 ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面 2014年11月11日 — 如图, ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O的直径,AD=6,那么AB的值为( ) A.3 B.2∵AB=BC,∴∠BAC=∠C,∵∠ABC=120°,∴∠BAC=∠C=30°,∵AD为直径,AD=6,∴∠ABD=90°,∵∠D=30 °,∴AB 百度首页 如图, ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O的
.jpg)
如图,BD、CD分别是三角形ABC的内角 角ABC、角ACB的
如图,BD、CD分别是三角形ABC的内角 角ABC、角ACB的平分线请说明角BDC与角A之间的等量关系是角BDC=90度+1/2角A 题目 举报 如图,在三角形ABC中,角ACB=90度,CD是角ACB的平分线,CD的垂直平分线分别交AC,CD,BC于点E,O,F2009年5月20日 — 已知,三角形ABC中,角BAC等于90度,AB=AC,M是AC边的中点等腰直角三角形ABC,AB=AC,角BAC=90度M为边AC的中点BM垂直AD交BC于D,垂足为E连接DM,求证角AMB=角DMC证明: 过C点做CF⊥AC,交AD延长线于点F ∴∠ACF=90度 ∵∠B已知,三角形ABC中,角BAC等于90度,AB=AC,M是AC边
.jpg)
如图,BD和CD分别平分 ABC的内角∠EBA和外角∠ECA,BD
4、试题分析:根据多边形的外角和为360°及题意,求出这个多边形的内角和,即可确定出多边形的边数 解:∵一个多边形的外角和是内角和的,且外角和为360°, ∴这个多边形的内角和为900°,即(n﹣2)•180°=900°, 解得:n=7, 则这个多边形的边数是7, 故选C考点:多边形内角与外角2014年9月17日 — (2014?常德)如图,已知 ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=80∵ ABC三个内角的平分线交于点O,∴∠ACO=∠BCO,在 COD和 COB中,CD=CB∠OCD=∠OCBCO=CO,∴ COD≌(2014?常德)如图,已知 ABC三个内角的平分线交于点O

已知:如图,在 ABC中,AB=AC,点D,E分别在边AC
已知:如图,在 ABC中,AB=AC,点D,E分别在边AC,AB上,且∠ ABD=∠ ACE,BD与CE相交于点O求证:(1)OB=OC;(2)BE=CD (1)证明:∵AB=AC, ∴∠ABC=∠ACB; ∵∠ABD=∠ACE, ∴∠OBC=∠OCB, ∴OB=OC (2)证明:如图, A E D 2011年11月2日 — 如图,在三角形ABC中,AB=AC,角BAC=120度,AC的垂直平分线EF交AC于点E,交BC于点F,求证:BF=2CF证明:连接AF∵EF是AC的垂直平分线∴AF=CF∵∠BAC=120°,AB=AC∴∠B=∠C=30°∴∠C=∠CAF=30°∴∠BAF=90 如图,在三角形ABC中,AB=AC,角BAC=120度,AC的
.jpg)
如图,在三角形ABC中,角BAC=120度,AB=AC,点D在BC上
如图,在三角形ABC中,角BAC=120度,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA 1试求角DAE的度数 2如果把试题中AB=AC的条件去掉,其余条件不变,那么角DAE的度数会改变吗?为什么?1 如图所示,圆O是三角形ABC的外接圆,角BAC与角ABC的平分线相交于点I,延长AI交圆O与点D,连接BD,DC若圆O的半径为10cm,角BAC=120度求三角形BAC面积的最大值 2 如图所示,圆O是三角形ABC如图所示,圆O是三角形ABC的外接圆,角BAC与角ABC的平分
.jpg)
如图,在三角形ABC中,AB=AC,作业帮
因为 AB=AC,角A=36度 所以 角ABC=角ACB=72度 因为 CD平分角ACB 所以 角BCD=角DCA=36度 因为 角A=36度 所以 角BCD=角A 因为 角DBC=角ABC 所以 三角形CDB相似于三角形ABC 所以 AB/BC=BC/BD 因为 角DCA=36度,角A=36度 所以 角DCA=角A2021年10月28日 — 如图,已知在三角形ABC中,角BAC等于90度,AB=AC,点D在边BC上,以AD为边作正方形ADEF,联结CF,CE(1)求证FC垂直于BC(2)如果BD=AC,求证 如图,已知在三角形ABC中,角BAC等于90度,AB=AC,点D在边BC上,以AD为边作正方形ADEF,联结CF,CE(1)求证FC垂直于BC(2)如果BD=AC,求证CD=CE 展开如图,已知在三角形ABC中,角BAC等于90度,AB=AC,点D在
.jpg)
如图所示,在三角形ABC中,角ABC=90度,AC=BC,D为
(1)证明:如图,连接CD,交AB于点F,AD=BD点C和点D均在线段AB的垂直平分线上直线CD为线段AB的垂直平分线为等腰直角三角形(2)如(1)中图所示若,则线段AE的长为1(1)连接CD,交AB于点F,则由线段垂直平分线的判定定理可得,直线CD是线段AB的 如图,在等腰三角形ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;② OPC是等边三角形;③AC=AO+AP;④ABC OCP S =S四边形其中所有正确结论的序号为( )P AB D A ①②③如图,在等腰三角形ABC中,AB=AC,∠BAC=120°,AD⊥
.jpg)
《圆》的计算及证明题之中考真题精选汇编(1) 百度文库
3.如图,圆内接四边形ABCD的对角线AC,BD交于点E,BD平分∠ABC,∠BAC=∠ADB 4.如图,已知⊙O是等边三角形ABC的外接圆,连接CO并延长交AB于点D,交⊙O于点E,连接EA,EB . (1)写出图中一个度数为30°的角:,图中与 ACD全等的
安徽生石灰陵机械制造厂
--半碳酸钙破煤碎机
--方解石矿方解石打粉生产线
--混凝土生产流程混凝土生产流程混凝土生产流程
--悬辊机价格唐山悬辊机价格唐山悬辊机价格唐山
--悬辊磨粉机产量550TH
--办采矿许可证后到林业办哪
--请问我想加工重碳酸钙粉有销路吗
--办理矿用的申请
--启东长三角上海一小时经济圈
--高岭土雷蒙磨器
--无锡碎煤机
--首矿大昌石灰石粉碎机材料有限公司新建发电厂
--火电厂燃料碎煤机技术
--ss的粒径为1mm选用多大的筛网
--锥破机价格
--vsi雷蒙磨叶轮旋转方向
--欧版磨粉机控制算法
--大型立磨案例
--硅灰石制粉生产线有什么特点
--红枣干磨超微粉碎机
--白泥滩产沙设备
--花岗岩加工设备磨粉机
--如何购买柳钢的水渣
--用什么机器生产腻子粉
--重钙矿石磨粉机轴承更换方法
--上海HP 磨煤机
--唐山滑石粉研磨机配件商店
--露天石材加工雷蒙磨
--红石灰石岩粉体加工设备
--










